score dial
2019-09-18
|~3 min read
|483 words
Given a score within a range, how could we visualize that on a dial? That was what I got to work on recently and it turned out to be a ton of fun!

(The animation was a late addition, but it really makes a difference. A big thanks to Justin who suggested I could calculate an incrementing score to re-render the element and give the effect of it filling up.)
Observations And Lessons
A few observations from the experience:
First and foremost: to all those folks who asked when we’d use trigonometry in the real world… I found the answer
Secondly, brushing off those trigonometry and geometry lessons from middle school turned out to be surprisingly fun.
Two resources in particular I used heavily:
- Triangle Calculator: Triangle Calculator
- Degrees to Radians Calculator: Degrees to Radians conversion
Third, a lot of the implementation required understanding where on the edge of the circle I was given the score. I ended up calculating that thanks to the “parametric equation” for a circle which I found, as usual via StackOverflow1
The one part of magic that I never quite understood was why I reversed the sign on the Y coordinate. I’m sure it has something to do with the direction of rotation and where I’m starting from, but still, I couldn’t quite work through it.
const calculateEdgeCoordinates = (internalAngle) => {
// Uses the Parametric Equation for a circle: https://stackoverflow.com/a/839931/9888057
const xCoord = ORIGIN.X + RADIUS * Math.cos(internalAngle)
const yCoord = ORIGIN.Y - RADIUS * Math.sin(internalAngle)
return { xCoord, yCoord }
}Fourth, context matters. A triangle is not a triangle if it’s in a different quadrant. Wait, what?
Just kidding. It’s still a triangle. It’s just more than that, because where it is matters. For example, the ending point for the Very Low score (~40, ~7) initially tripped me up.
Initially, when I calculated the triangle created by the hypotenuse between the origin and the point (~40, ~7), I only looked at the lengths of the sides to calculate the angles.
This was the right triangle, but in my quadrant, it put the edge at (~60, ~7).
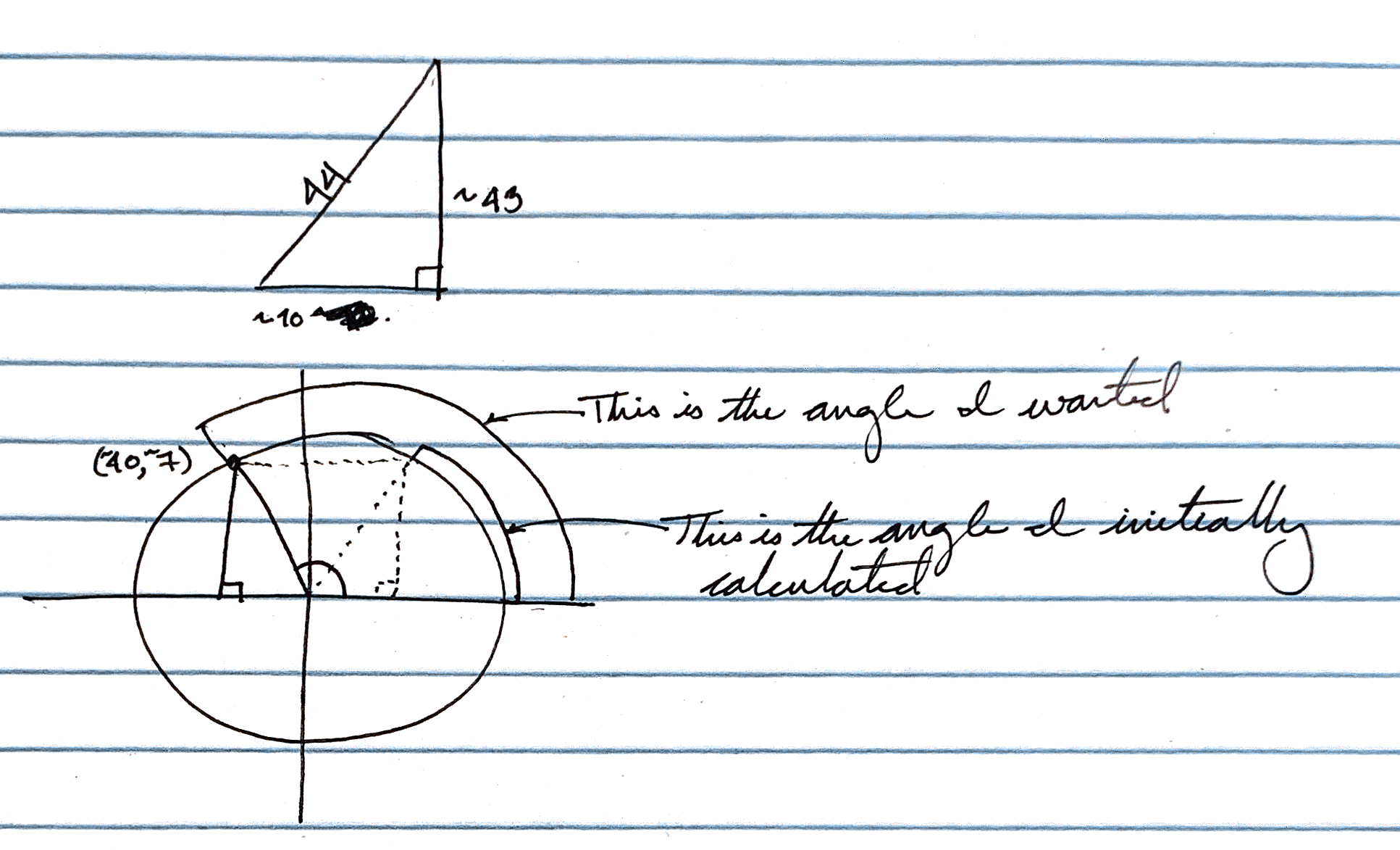 That’s clearly not right and once I put it on paper, I could see that clearly. Mirroring the triangle over the Y-axis and using my angle identities I was able to arrive at the correct distance.
That’s clearly not right and once I put it on paper, I could see that clearly. Mirroring the triangle over the Y-axis and using my angle identities I was able to arrive at the correct distance.
Conclusion
Overall, I’m very pleased with how this turned out and had a ton of fun along the way — even if I am sure I exhausted my wife and friends with all of my questions. With that in mind, I’ll likely be taking a bit of a break from the trig and SVGs.
I’ve posted the full code to Github2
Footnotes
Hi there and thanks for reading! My name's Stephen. I live in Chicago with my wife, Kate, and dog, Finn. Want more? See about and get in touch!